Process capability analysis is a crucial tool for businesses to assess and evaluate the efficiency and quality of their product development processes. By measuring and analyzing the capability of a process, businesses can determine how well it meets predetermined specifications and identify areas for improvement. In this comprehensive guide, we will explore the concept of process capability, its importance, and how it can be calculated.

What is Process Capability?

At its core, a process is a combination of tools, resources, and personnel working together to produce a specific product or output. Ideally, a process should consistently produce outputs that meet the desired specifications. However, it is inevitable that there will be some variation in the output of a process. Process capability analysis helps measure this variation and assesses how well a process meets the specified requirements.

Process capability provides valuable insights into two key aspects of a process. Firstly, it measures the variability in the output, indicating how consistent the process is in delivering the desired results. Secondly, it compares the capability of the process to the predetermined specifications, allowing businesses to identify areas that need improvement and optimize production efficiency.

To perform a process capability analysis, it is important to use data from an in-control process. An in-control process refers to a process where the output measurements follow a normal bell-curve distribution over time. Using reliable and accurate data sets is essential for the success of process capability analysis.

Capability vs. Stability

Before delving deeper into process capability analysis, it is crucial to understand the distinction between capability and stability. A process is considered capable if it consistently delivers outputs that meet the specified requirements. On the other hand, stability refers to the absence of non-random or special causes of variation in a process. While stability is not a requirement for assessing process capability, it is necessary to determine whether a process is capable.

The Capability Index, CPK

The capability index, CPK, is a statistic that measures the ability of a process to consistently deliver output within the specified limits. It provides crucial information about how well a process meets the defined criteria and enables businesses to assess production efficiency.

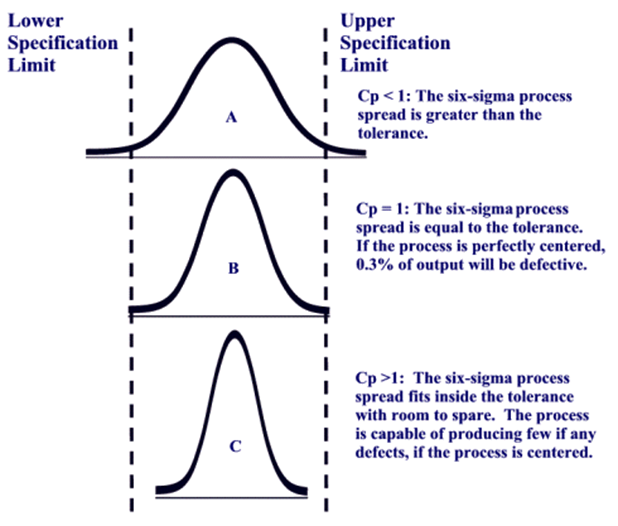
The CPK value ranges from less than 1.00 to greater than 1.67. A CPK value less than 1.00 indicates poor capability and implies that the process is not capable of meeting the specified requirements. A CPK value between 1.00 and 1.67 is considered fair, indicating that the process has some capability but may require improvements. Finally, a CPK value greater than 1.67 signifies excellent capability, indicating that the process consistently produces output that meets the specified limits. A CPK value of 2 is often associated with a six sigma process, which is considered highly capable and efficient.

Formula for CP, CPK, PP, and PPK

To calculate process capability indices, various formulas are used. The primary indices are CP, CPK, PP, and PPK. These indices provide insights into the spread and centering of a process. The formulas for these indices are as follows:

• CP = (USL – LSL) / (6 * sigma)
• CPK = min((USL – mean) / (3 * sigma), (mean – LSL) / (3 * sigma))
• PP = (USL – LSL) / (6 * sigma)
• PPK = min((USL – mean) / (3 * sigma), (mean – LSL) / (3 * sigma))

In these formulas, USL represents the upper specification limit, LSL represents the lower specification limit, mean represents the process mean, and sigma represents the process standard deviation. These indices provide a quantitative measure of a process’s capability and enable businesses to make informed decisions about process improvement.

Interpreting Process Capability

Interpreting the results of a process capability analysis is crucial for businesses to understand the current state of their processes. The acceptance of a process’s capability is typically determined based on the CPK value. A CPK value greater than 1.33 is generally considered acceptable, indicating that the process can consistently meet the specified requirements.

However, it is essential to consider other factors, such as customer expectations and industry standards, when evaluating process capability. The CPK value provides a quantitative measure, but it is important to align it with qualitative aspects and customer satisfaction.

Advantages of a Capable Process

A capable process offers numerous advantages for businesses. Let’s explore the key benefits of having a capable process:

1. Consistency: A capable process consistently produces outputs that meet the specified requirements, ensuring consistency in product quality.
2. Uniformity: With low variability, a capable process produces outputs that are highly uniform, reducing the likelihood of defects or variations.
3. Cost Savings: A capable process with low variability reduces the need for extensive in-process and final inspections, saving time and resources.
4. Reduced Defects: A capable process results in minimal or no defects, minimizing scrap, rework, and repair levels.
5. Improved Customer Satisfaction: By meeting the specified requirements consistently, a capable process ensures customer satisfaction and enhances the brand’s reputation.

It is important to note that achieving process capability requires ongoing communication with customers and aligning the process specifications with their requirements and expectations.

How to Measure and Calculate Process Capability

To measure and calculate process capability, businesses need to follow a systematic approach. Here are the steps involved in conducting a process capability analysis:

1. Collect Data: Gather data from an in-control process, ensuring it represents the typical operation of the process.
2. Determine Specification Limits: Identify the upper and lower specification limits based on the desired requirements and customer expectations.
3. Calculate Process Mean: Calculate the mean of the process data to determine the centering of the process.
4. Calculate Process Standard Deviation: Compute the standard deviation of the process data to measure the variability.
5. Calculate CP: Use the formula (USL – LSL) / (6 * sigma) to calculate the CP value, which represents the spread of the process.
6. Calculate CPK: Use the formula min((USL – mean) / (3 * sigma), (mean – LSL) / (3 * sigma)) to calculate the CPK value, which considers both spread and centering.
7. Interpret the Results: Evaluate the CP and CPK values to determine the capability of the process and assess if it meets the specified requirements.
8. Continuous Improvement: Based on the analysis, identify areas for improvement and implement measures to enhance process capability.

It is crucial to note that process capability analysis is an ongoing process, and continuous improvement efforts are essential to maintain and enhance process capability over time.

Conclusion

Process capability analysis is a vital tool for businesses to assess and evaluate the efficiency and quality of their product development processes. By measuring and analyzing the capability of a process, businesses can determine how well it meets the specified requirements and identify areas for improvement. Process capability indices such as CP and CPK provide quantitative measures of a process’s capability and enable businesses to make data-driven decisions.

Achieving process capability requires ongoing monitoring, evaluation, and improvement efforts. By continuously striving for process improvement, businesses can enhance their competitiveness, meet customer expectations, and ensure consistent product quality. Process capability analysis is a valuable tool that empowers businesses to optimize their processes and stay ahead of the competition.